Hi all,
In the solution, it states that triangle CGI is isosceles because CG = DI. I know that it probably meant that CG = CI, but even then, how is CG = CI? I'm just curious.
Thanks,
Roger Chen
Hi all,
In the solution, it states that triangle CGI is isosceles because CG = DI. I know that it probably meant that CG = CI, but even then, how is CG = CI? I'm just curious.
Thanks,
Roger Chen
Hew Roger!
That was indeed a typo. It is now fixed. Thanks for letting us know!
As to why the statement is true, consider the following: $CA$ is parallel to line $DE$ (since $\triangle ABC$ is isosceles, and we can look at their angles). Then we can reflect pentagon $ABCDE$ through line $CA$ to obtain the following diagram:
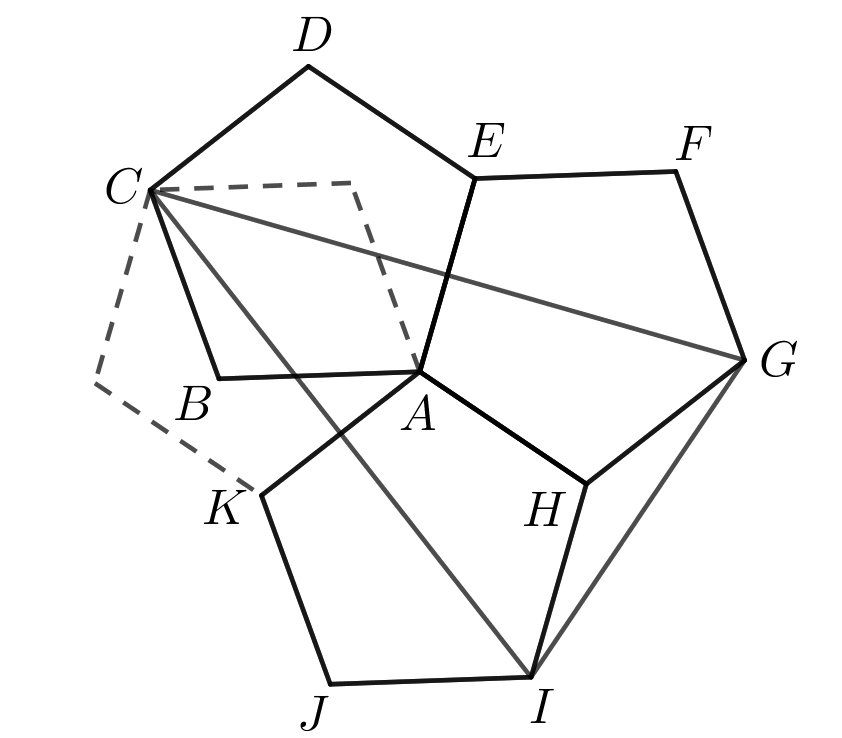
Then both $CG$ and $CI$ are lines that join opposite vertices of two adjacent regular pentagons of the same size, and therefore have the same length.