From the week of December 4 to December 8 we chose Tuesday's problem (that you can find here):
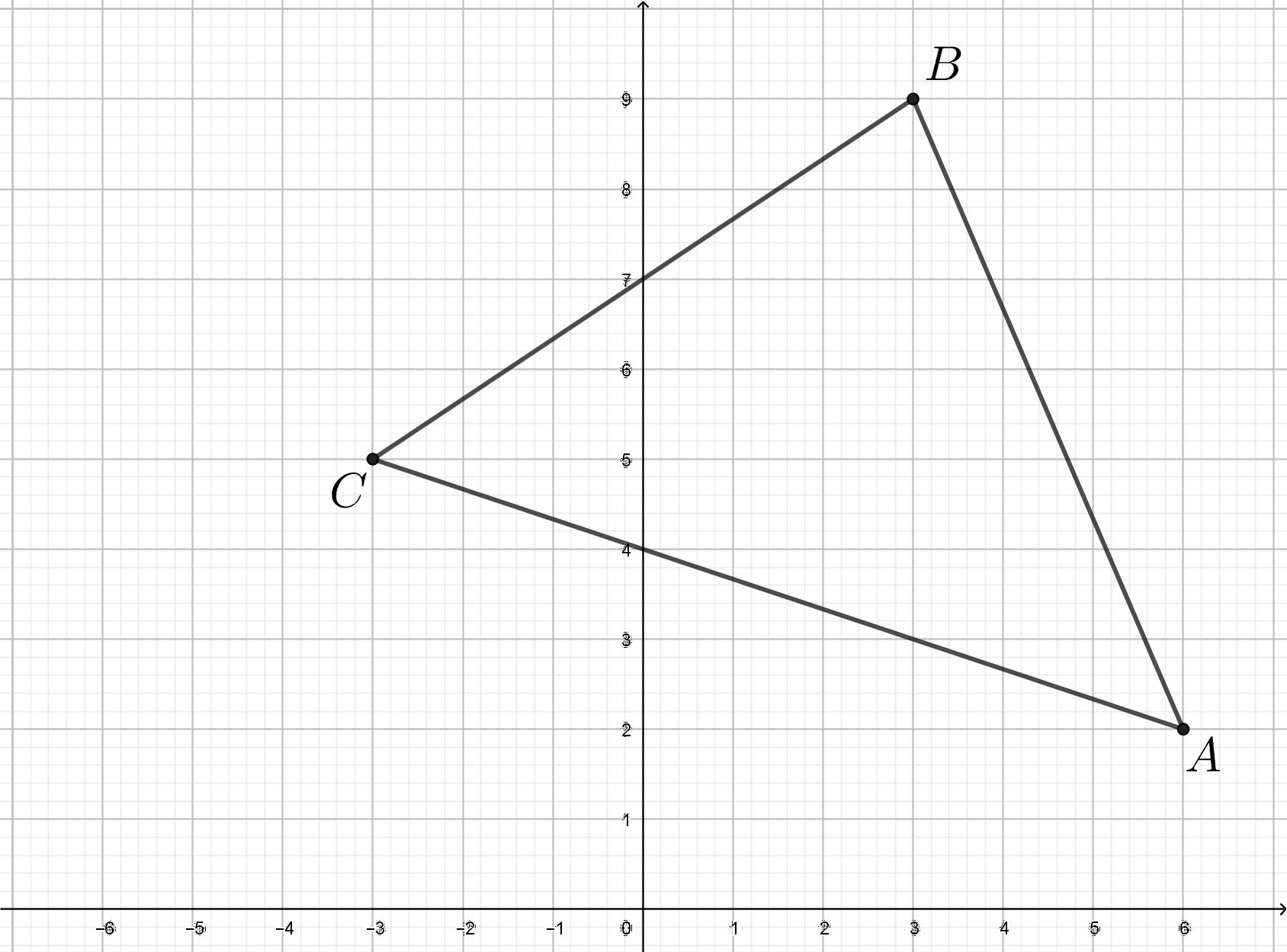
Daisy graphed points $A = (6,2)$, $B=(3,9)$ and $C = (-3,5)$ on a plane to form $\triangle ABC$. She then reflected all three points over the $y$-axis to obtain three new points $A'$, $B'$ and $C'$. Triangles $ABC$ and $A'B'C'$ overlap to form a butterfly-like figure. What is the area of the butterfly?
31% of the students who tried the problem got it right on their first attempt.
Daisy starts by graphing the following triangle:
Then she reflects all three points over the $y$-axis, that is, she pretends the $y$-axis is a mirror, to come up with new points that form a second triangle:
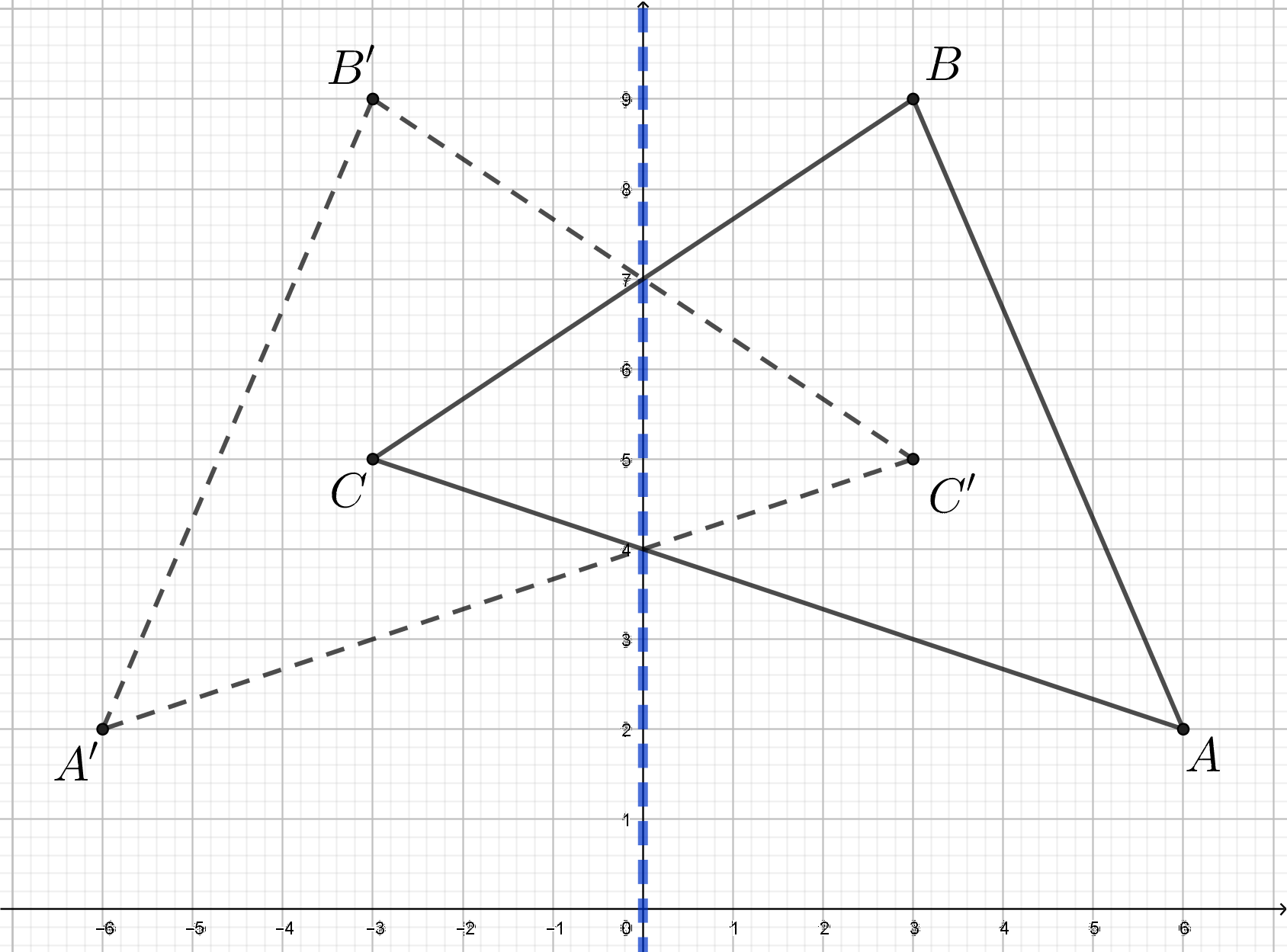
When reflecting points over the $y$-axis we want to be careful to keep the same $y$-coordinate, and change the sign of the $x$-coordinate of each point. So, for example, point $A = (6,2)$ reflects to point $A'=(-6,2)$.
After Daisy added some color to her diagram. she noticed the whole figure indeed looked like a butterfly!

A popular answer was $9$ which is the area of just the overlap of the two triangles, not the whole butterfly. Finding the area of the butterfly could seem tricky at first, however, notice it fits perfectly inside a rectangle:

How big is that rectangle around the butterfly? How can we use that rectangle to make it easier to find the area of the butterfly?
Share your thoughts and questions below!