
For the first problem, I blindly guessed an answer because I was running out of time, but I do not know why this is the correct solution. For the second problem, I'm not sure where I did something wrong, is it just an estimation error?


For the first problem, I blindly guessed an answer because I was running out of time, but I do not know why this is the correct solution. For the second problem, I'm not sure where I did something wrong, is it just an estimation error?
First (probability) question: There are $8\cdot 7 = 56$ total ways to choose a first and second point. Note, however, that the only way two points can be distance $1$ from each other is if they are adjacent (next to each other). Thus, there are $8\cdot 2 = 16$ ways to choose two adjacent points (any of the $8$ points has $2$ points adjacent to it). This gives a probability of $\dfrac{16}{56} = \dfrac{2}{7}$.
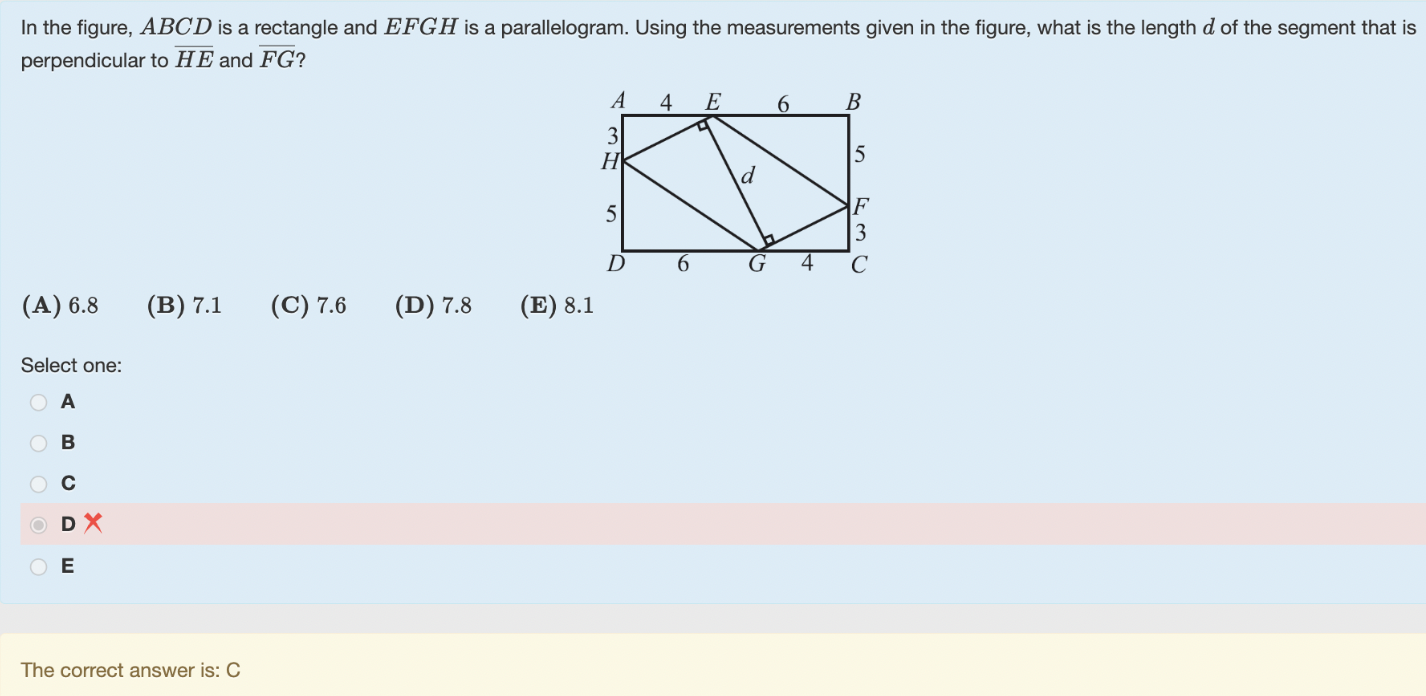
Second (geometry) question: Let me give a hint for this one, cause it's a good one to practice solving. Remember that the area of a parallelogram is base times height. Therefore, since we know the segment with length $d$ is perpendicular to $\overline{FG}$ and $\overline{EH}$, we know the area of parallelogram $EFGH$ is $[EFGH] = FG\cdot d$. Note you should be able to find the length $FG$ fairly easily. Then note that we can also calculate the area $[EFGH]$ a different way (hint: try to start with area of the full rectangle and subtract what you don't want).
Hope this helps! Let us know if you have additional questions.
Thank you for your solutions! They did help with the two questions. I have another 2 questions for this week. I did not find a solution to the first problem online. I am confused about the second question, as the solution implies that each region can only be hit once, but this is not mentioned in the question prompt.
Thank you!

Let me again give some hints to help.
1st Question (probability): The hardest part of this problem is determining the probability that a dart (on a single throw) lands in the various regions. The probability is proportional to the area of each region. To start, notice that the inner circle has an area of $\pi 3^2 = 9\pi$, the full circle has area $\pi\cdot 6^2 = 36\pi$, and therefore the outer ring has probability $36\pi - 9\pi = 27\pi$.
Therefore, each of the inner regions (with points 1, 2, and 2) have probability $\dfrac{9\pi \div 3}{36\pi} = \dfrac{1}{12}$ and each of the outer regions (with points 2, 1, and 1) have probability $\dfrac{27\pi\div 3}{36\pi} = \dfrac{1}{4}$.
Some hints to continue from here: (i) What is the probability a single throw is 1 (odd)? What is the probability a single throw is 2 (even)? How can the sum of the two throws be odd?
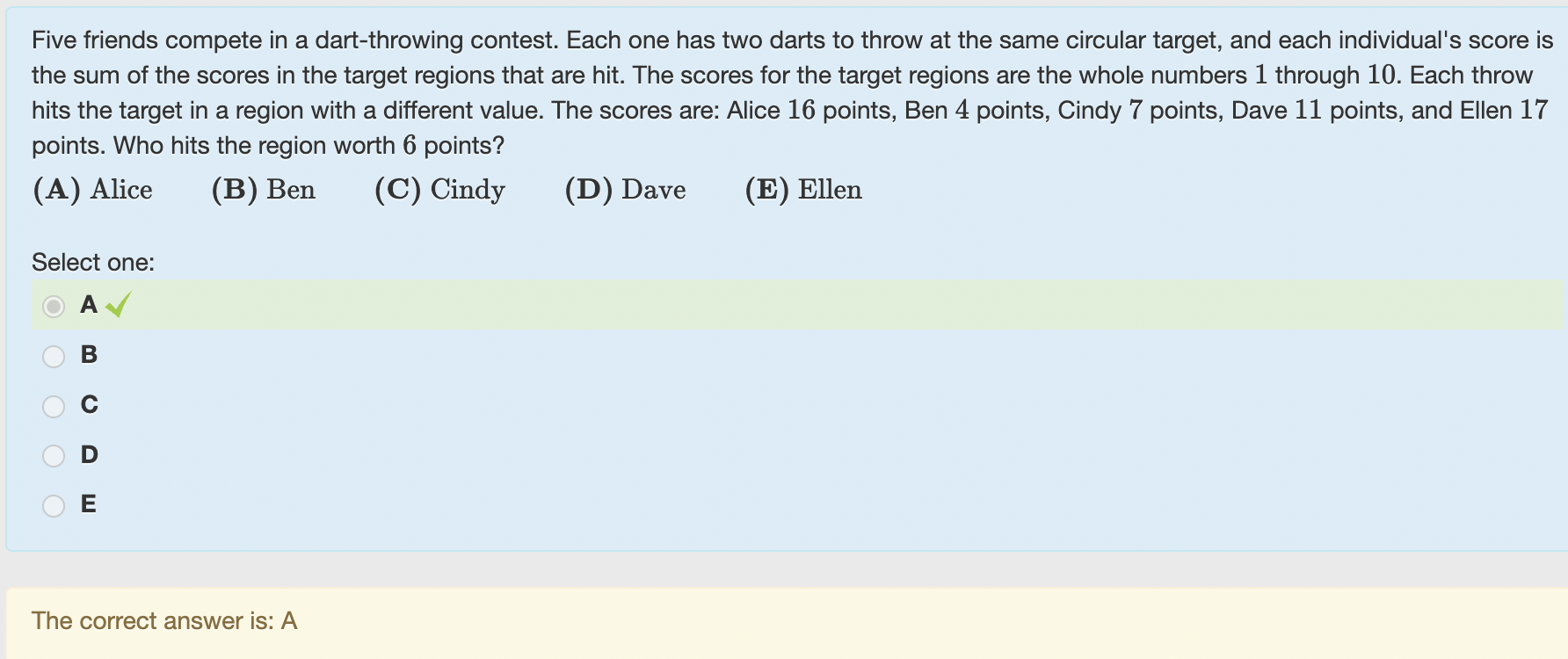
2nd Question (arithmetic & logic): Actually I think the problem does say that each region can only be hit once, because it says "Each throw hits the target in a region with a different value." Note: Even though both problems are about darts, they really are not very similar to each other, since the second one doesn't really have any probability involved.
Hope this helps!