For the first problem, I blindly guessed an answer because I was running out of time, but I do not know why this is the correct solution. For the second problem, I'm not sure where I did something wrong, is it just an estimation error?
Discussion Forum
AMC 8 Mock questions
AMC 8 Mock questions
Re: AMC 8 Mock questions
First (probability) question: There are $8\cdot 7 = 56$ total ways to choose a first and second point. Note, however, that the only way two points can be distance $1$ from each other is if they are adjacent (next to each other). Thus, there are $8\cdot 2 = 16$ ways to choose two adjacent points (any of the $8$ points has $2$ points adjacent to it). This gives a probability of $\dfrac{16}{56} = \dfrac{2}{7}$.
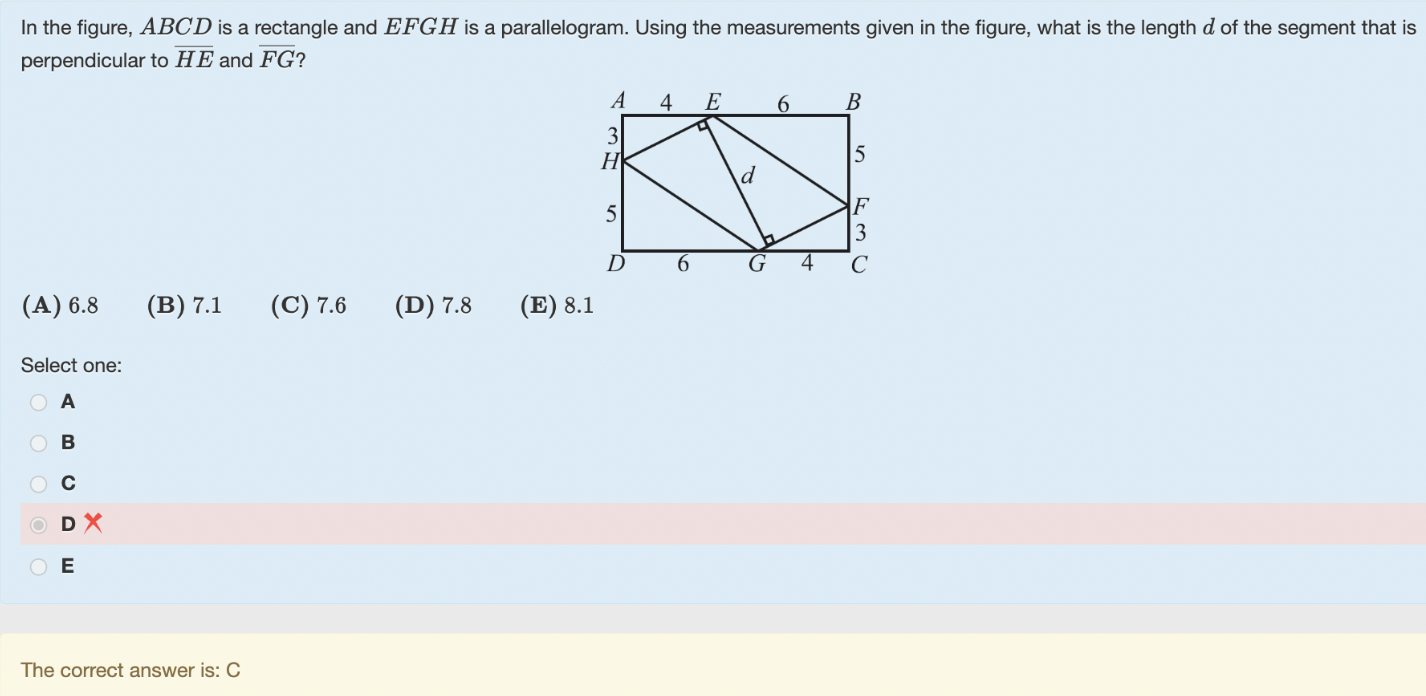
Second (geometry) question: Let me give a hint for this one, cause it's a good one to practice solving. Remember that the area of a parallelogram is base times height. Therefore, since we know the segment with length $d$ is perpendicular to $\overline{FG}$ and $\overline{EH}$, we know the area of parallelogram $EFGH$ is $[EFGH] = FG\cdot d$. Note you should be able to find the length $FG$ fairly easily. Then note that we can also calculate the area $[EFGH]$ a different way (hint: try to start with area of the full rectangle and subtract what you don't want).
Hope this helps! Let us know if you have additional questions.
Re: AMC 8 Mock questions
Thank you for your solutions! They did help with the two questions. I have another 2 questions for this week. I did not find a solution to the first problem online. I am confused about the second question, as the solution implies that each region can only be hit once, but this is not mentioned in the question prompt.
Thank you!
Re: AMC 8 Mock questions
Let me again give some hints to help.
1st Question (probability): The hardest part of this problem is determining the probability that a dart (on a single throw) lands in the various regions. The probability is proportional to the area of each region. To start, notice that the inner circle has an area of $\pi 3^2 = 9\pi$, the full circle has area $\pi\cdot 6^2 = 36\pi$, and therefore the outer ring has probability $36\pi - 9\pi = 27\pi$.
Therefore, each of the inner regions (with points 1, 2, and 2) have probability $\dfrac{9\pi \div 3}{36\pi} = \dfrac{1}{12}$ and each of the outer regions (with points 2, 1, and 1) have probability $\dfrac{27\pi\div 3}{36\pi} = \dfrac{1}{4}$.
Some hints to continue from here: (i) What is the probability a single throw is 1 (odd)? What is the probability a single throw is 2 (even)? How can the sum of the two throws be odd?
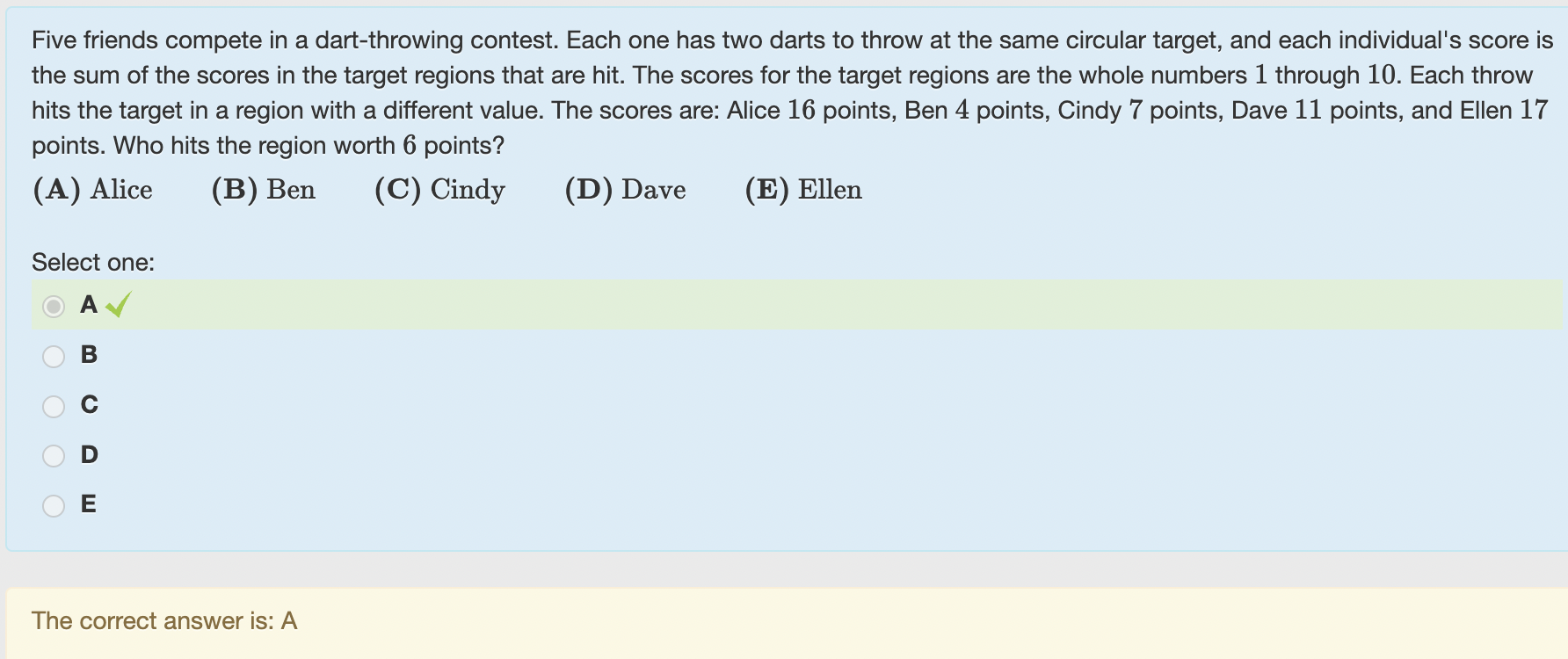
2nd Question (arithmetic & logic): Actually I think the problem does say that each region can only be hit once, because it says "Each throw hits the target in a region with a different value." Note: Even though both problems are about darts, they really are not very similar to each other, since the second one doesn't really have any probability involved.
Hope this helps!