From the week of October 2 to October 6 we chose Tuesday's problem (that you can find here):
Roger went to the beach with his parents. As he was walking, he left a trail of footprints on the sand, one right after another. He noticed then, that his shadow was $10$ feet long (as it turns out, Roger's feet are exactly $1$ foot long). According to his last measurements, he is $5$ feet and $3$ inches tall. What is the angle of elevation of the Sun? Round your answer to the nearest degree.

32% of the students who tried the problem got it right on their first attempt.
The problem is telling us how tall is Roger, and how long is his shadow. We then want to use that information to figure out "the angle of elevation of the Sun", that is, if we were to place a long stick on the ground that is pointing right at the Sun, what is the angle between the ground and the stick?
For a problem like this, a great place to start is by making a drawing. Imagine "the stick" being stuck on the sand right where Roger's shadow ends and so that it also touches Roger's head. That would produce a drawing like this:
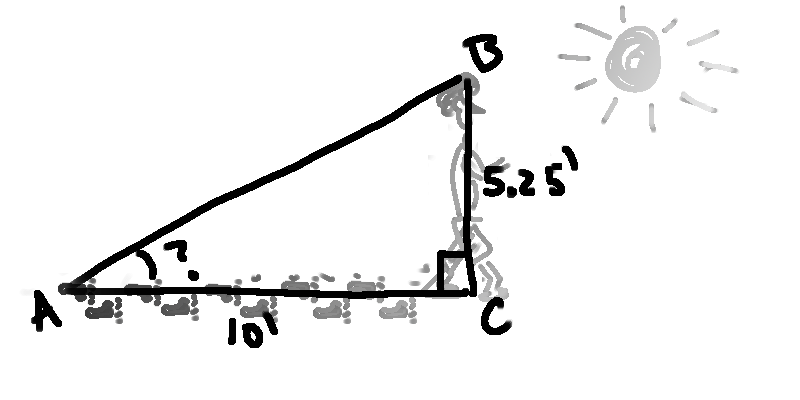
Note how we can now "see" a right triangle that we can use to figure our the angle between the sand and the stick. Now that we turned the word problem into a geometry problem, what do you think we can do to finish it?
Share your thoughts and questions below!