A common game of chance is called Roulette. A ball is rolled around a circular disk (called the wheel) containing some numbers. Players can bet on where the ball comes to a rest, such as one a red spot or on a specific number. A simplified Roulette wheel is shown below.
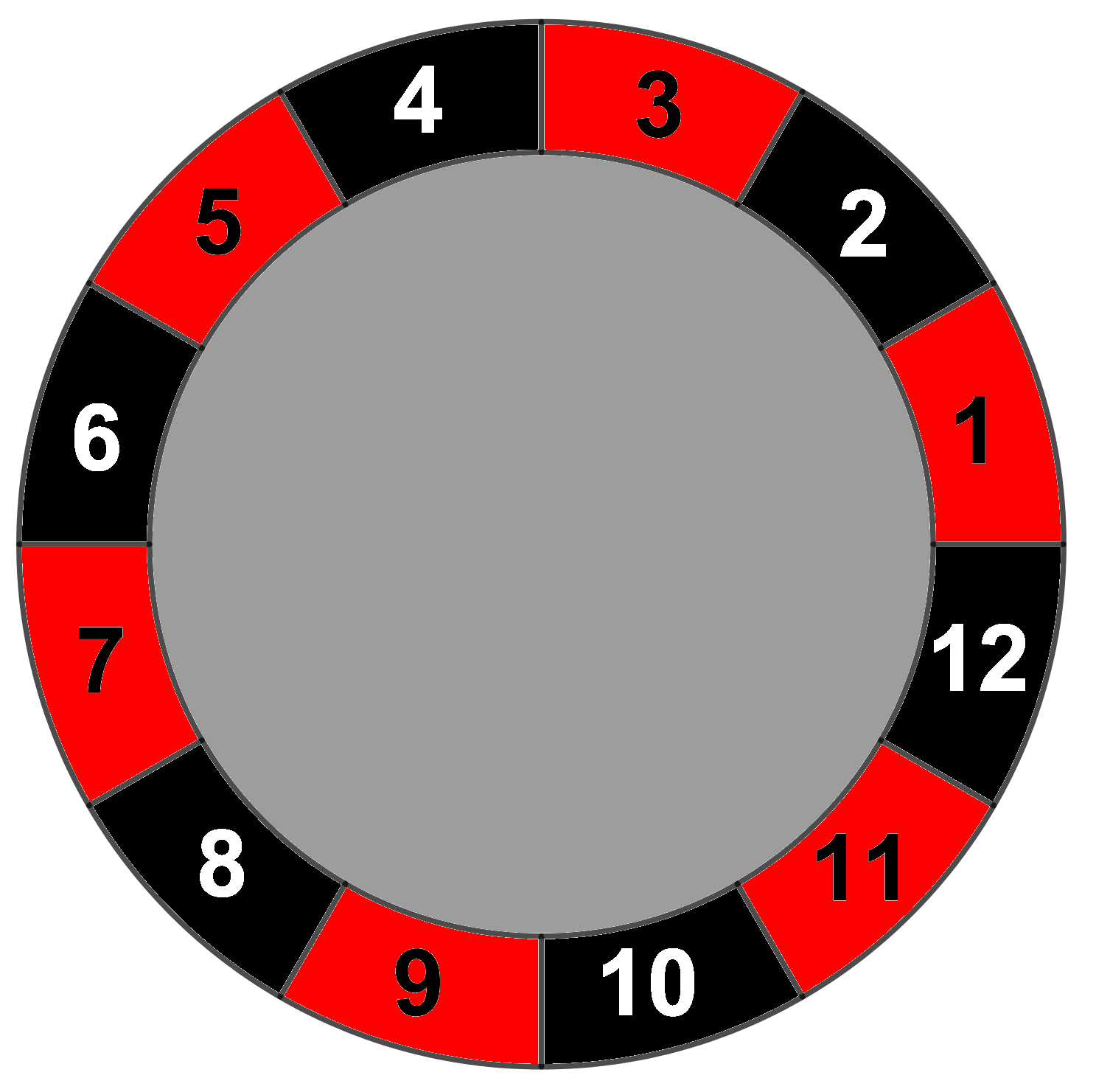
For this discussion we'll focus on betting that the ball will stop on red. The following bet is made:
- You can bet $N$ dollars that the ball will land on red.
- If you are correct you win $2N$ dollars (you double your money), but if you are incorrect you win $\$0$ (you lose the money you bet).
After explaining the game to your friend Peter, he devises the following strategy, which he claims will allow you to always win $\$1$!
- First bet $\$1$ on red. If you win you have won $\$1$ (remember you spent $\$1$ on the bet).
- If you lose bet $\$2$ on red.
- If you lose again bet $\$4$ on red.
- If you lose again bet $\$8$ on red.
- Etc. Continuing to bet until the ball lands on red.
Explain how Peter's strategy works in theory. On the other hand, explain how Peter's strategy does not work in practice (in the real world). If it did, we would all be at casinos playing Roulette right now!
Please share any thoughts or questions you have below. We'll monitor the responses and give our thoughts as well!
