2017 AMC 8 Questions
Below you will find the questions from the 2017 AMC 8. Answers are available in the attached file. Feel free to share your thoughts and solutions to the problems!
You can take a simulated version of this exam (and all previous exams) on our practice page found by clicking here.
Note: All of these questions are copyrighted by American Mathematics Competitions at Mathematical Association of America.
Question 1
Which of the following values is largest?
$\textbf{(A) }2+0+1+7\\ \textbf{(B) }2 \times 0 +1+7\\ \textbf{(C) }2+0 \times 1 + 7\\ \textbf{(D) }2+0+1 \times 7\\ \textbf{(E) }2 \times 0 \times 1 \times 7$
Question 2
Alicia, Brenda, and Colby were the candidates in a recent election for student president. The pie chart below shows how the votes were distributed among the three candidates.
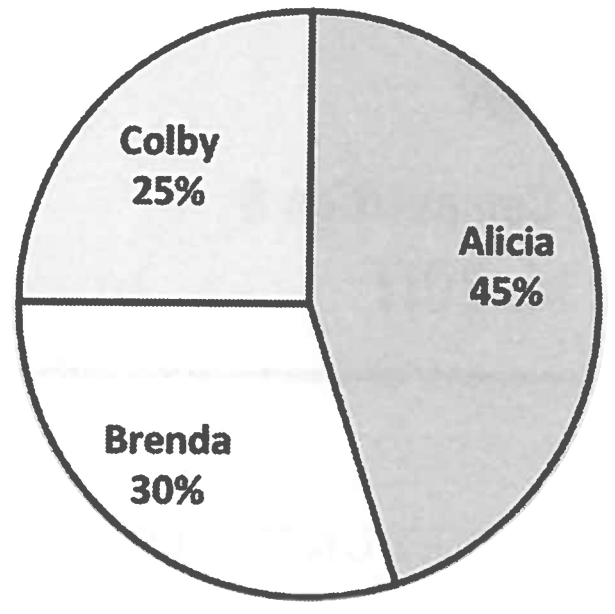
If Brenda received $36$ votes, then how many votes were cast all together?
$\textbf{(A) }70\qquad\textbf{(B) }84\qquad\textbf{(C) }100\qquad\textbf{(D) }106\qquad\textbf{(E) }120$
Question 3
What is the value of the expression $\sqrt{16\sqrt{8\sqrt{4}}}$?
$\textbf{(A) }4\qquad\textbf{(B) }4\sqrt{2}\qquad\textbf{(C) }8\qquad\textbf{(D) }8\sqrt{2}\qquad\textbf{(E) }16$
Question 4
When $0.000315$ is multiplied by $7,928,564$ the product is closest to which of the following?
$\textbf{(A) }210\qquad\textbf{(B) }240\qquad\textbf{(C) }2100\qquad\textbf{(D) }2400\qquad\textbf{(E) }24000$
Question 5
What is the value of the expression $\displaystyle \frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8}{1+2+3+4+5+6+7+8}$?
$\textbf{(A) }1020\qquad\textbf{(B) }1120\qquad\textbf{(C) }1220\qquad\textbf{(D) }2240\qquad\textbf{(E) }3360$
Question 6
If the degree measures of the angles of a triangle are in the ratio $3:3:4$, what is the degree measure of the largest angle of the triangle?
$\textbf{(A) }18\qquad\textbf{(B) }36\qquad\textbf{(C) }60\qquad\textbf{(D) }72\qquad\textbf{(E) }90$
Question 7
Let $Z$ be a 6-digit positive integer, such as $247247$, whose first three digits are the same as its last three digits taken in the same order. Which of the following numbers must be a factor of $Z$?
$\textbf{(A) }11\qquad\textbf{(B) }19\qquad\textbf{(C) }101\qquad\textbf{(D) }111\qquad\textbf{(E) }1111$
Question 8
Malcolm wants to visit Isabella after school today and knows the street where she lives but doesn't know her house number. She tells him, "My house number has two digits, and exactly three of the following four statements about it are true."
(1) It is prime.
(2) It is even.
(3) It is divisible by $7$.
(4) One of its digits is $9$.
This information allows Malcolm to determine Isabella's house number. What is its units digit?
$\textbf{(A) }4\qquad\textbf{(B) }6\qquad\textbf{(C) }7\qquad\textbf{(D) }8\qquad\textbf{(E) }9$
Question 9
All of Marcy's marbles are blue, red, green, or yellow. One third of her marbles are blue, one fourth of them are red, and six of them are green. What is the smallest number of yellow marbles that Marcy could have?
$\textbf{(A) }1\qquad\textbf{(B) }2\qquad\textbf{(C) }3\qquad\textbf{(D) }4\qquad\textbf{(E) }5$
Question 10
A box contains five cards, numbered $1$, $2$, $3$, $4$, and $5$. Three cards are selected randomly without replacement from the box. What is the probability that $4$ is the largest value selected?
$\displaystyle \textbf{(A) }\frac{1}{10}\qquad\textbf{(B) }\frac{1}{5}\qquad\textbf{(C) }\frac{3}{10}\qquad\textbf{(D) }\frac{2}{5}\qquad\textbf{(E) }\frac{1}{2}$
Question 11
A square-shaped floor is covered with congruent square tiles. If the total number of tiles that lie on the two diagonals is $37$, how many tiles cover the floor?
$\textbf{(A) }148\qquad\textbf{(B) }324\qquad\textbf{(C) }361\qquad\textbf{(D) }1296\qquad\textbf{(E) }1369$
Question 12
The smallest positive integer greater than $1$ that leaves a remainder of $1$ when divided by $4$, $5$, and $6$ lies between which of the following pairs of numbers?
$\textbf{(A) }2\text{ and }19\qquad\textbf{(B) }20\text{ and }39\qquad\textbf{(C) }40\text{ and }59\qquad\textbf{(D) }60\text{ and }79\qquad\textbf{(E) }80\text{ and }124$
Question 13
Peter, Emma, and Kyler played chess with each other. Peter won $4$ games and lost $2$ games. Emma won $3$ games and lost $3$ games. If Kyler lost $3$ games, how many games did he win?
$\textbf{(A) }0\qquad\textbf{(B) }1\qquad\textbf{(C) }2\qquad\textbf{(D) }3\qquad\textbf{(E) }4$
Question 14
Chloe and Zoe are both students in Ms. Demeanor's math class. Last night they each solved half of the problems in their homework assignment alone and then solved the other half together. Chloe had correct answers to only $80\%$ of the problems she solved alone, but overall $88\%$ of her answers were correct. Zoe had correct answers to $90\%$ of the problems she solved alone. What was Zoe's overall percentage of correct answers?
$\textbf{(A) }89\qquad\textbf{(B) }92\qquad\textbf{(C) }93\qquad\textbf{(D) }96\qquad\textbf{(E) }98$
Question 15
In the arrangement of letters and numerals below, by how many different paths can one spell $AMC8$? Beginning at the $A$ in the middle, a path allows only moves from one letter to an adjacent (above, below, left, or right, but not diagonal) letter. One example of such a path is traced in the picture.
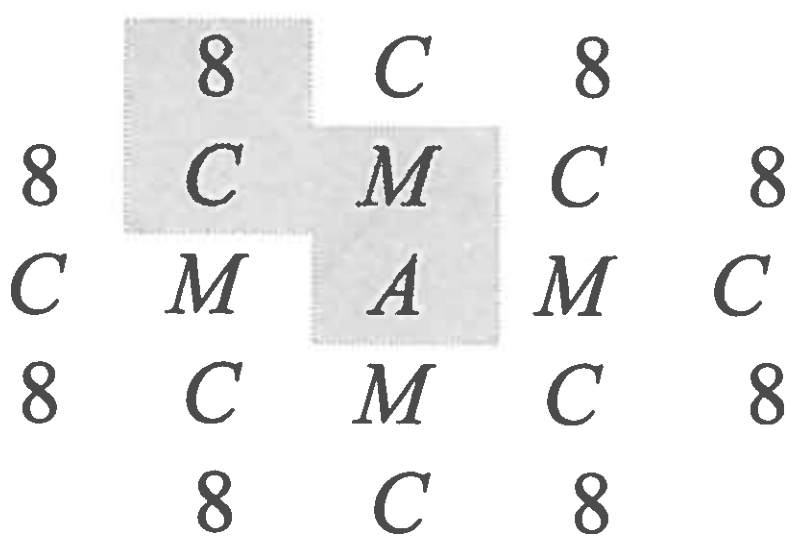
$\textbf{(A) }8\qquad\textbf{(B) }9\qquad\textbf{(C) }12\qquad\textbf{(D) }24\qquad\textbf{(E) }36$
Question 16
In the figure below, choose point $D$ on $\overline{BC}$ so that $\triangle ACD$ and $\triangle ABD$ have equal perimeters.
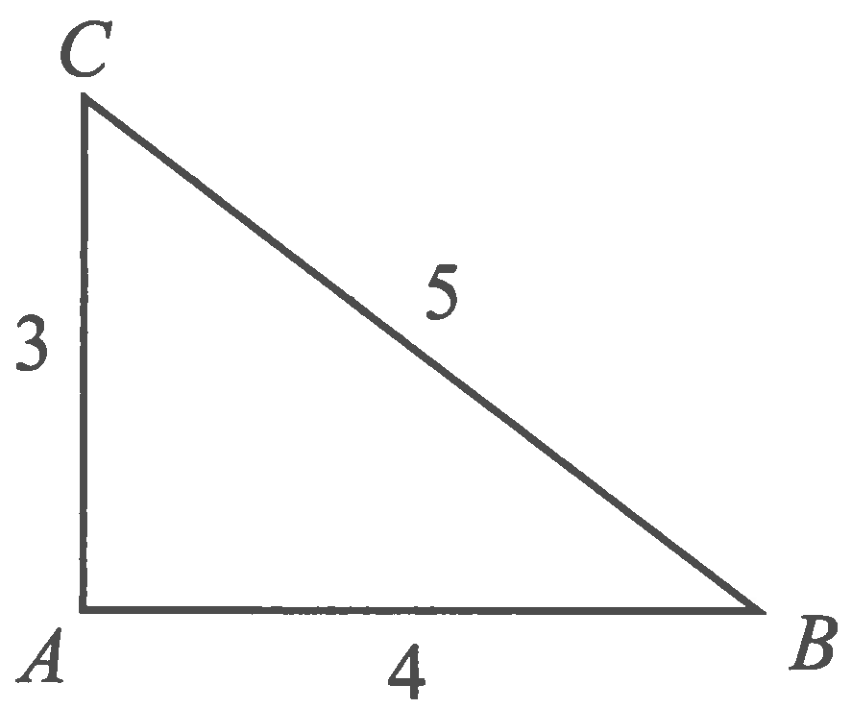
What is the area of $\triangle ABD$?
$\textbf{(A) }\frac{3}{4}\qquad\textbf{(B) }\frac{3}{2}\qquad\textbf{(C) }2\qquad\textbf{(D) }\frac{12}{5}\qquad\textbf{(E) }\frac{5}{2}$
Question 17
Starting with some gold coins and some empty treasure chests, I tried to put $9$ gold coins in each treasure chest, but that left $2$ treasure chests empty. So instead I put $6$ gold coins in each treasure chest, but then I had $3$ gold coins left over. How many gold coins did I have?
$\textbf{(A) }9\qquad\textbf{(B) }27\qquad\textbf{(C) }45\qquad\textbf{(D) }63\qquad\textbf{(E) }81$
Question 18
In the non-convex quadrilateral $ABCD$ shown below, $\angle BCD$ is a right angle, $AB=12$, $BC=4$, $CD=3$, and $AD=13$.
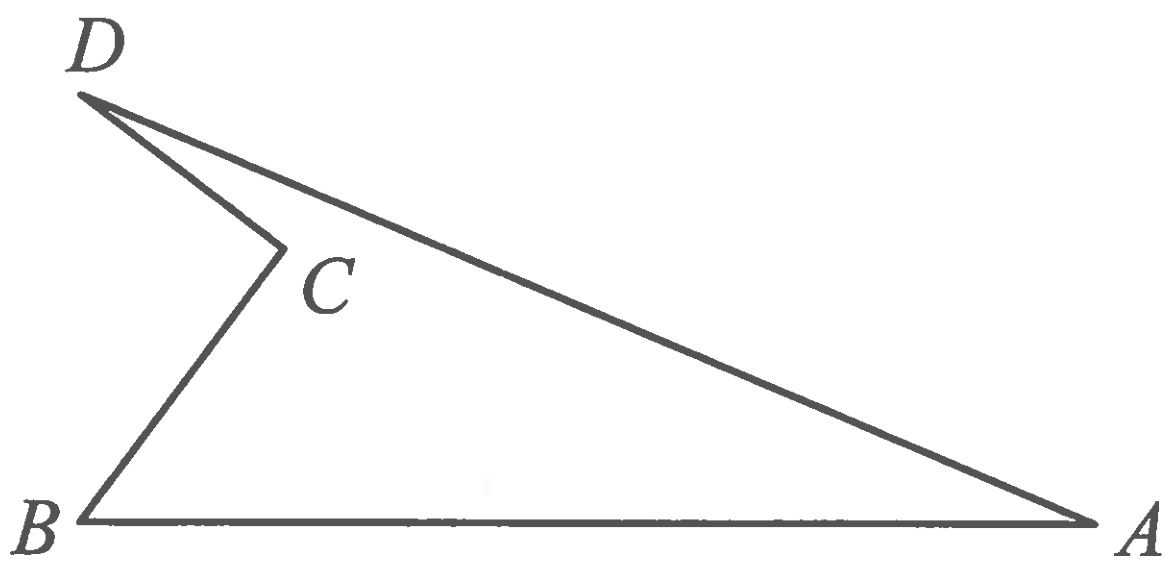
What is the area of quadrilateral $ABCD$?
$\textbf{(A) }12\qquad\textbf{(B) }24\qquad\textbf{(C) }26\qquad\textbf{(D) }30\qquad\textbf{(E) }36$
Question 19
For any positive integer $M$, the notation $M!$ denotes the product of the integers $1$ through $M$. What is the largest integer $n$ for which $5^n$ is a factor of the sum $98!+99!+100!$?
$\textbf{(A) }23\qquad\textbf{(B) }24\qquad\textbf{(C) }25\qquad\textbf{(D) }26\qquad\textbf{(E) }27$
Question 20
An integer between $1000$ and $9999$, inclusive, is chosen at random. What is the probability that it is an odd integer whose digits are all distinct?
$\displaystyle \textbf{(A) }\frac{14}{75}\qquad\textbf{(B) }\frac{56}{225}\qquad\textbf{(C) }\frac{107}{400}\qquad\textbf{(D) }\frac{7}{25}\qquad\textbf{(E) }\frac{9}{25}$
Question 21
Suppose $a$, $b$, and $c$ are nonzero real numbers, and $a+b+c=0$. What are the possible value(s) for $\displaystyle \frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|}$?
$\textbf{(A) }0\qquad\textbf{(B) }1\text{ and }-1\qquad\textbf{(C) }2\text{ and }-2\qquad\textbf{(D) }0,2,\text{ and }-2\qquad\textbf{(E) }0,1,\text{ and }-1$
Question 22
In the right triangle $ABC$, $AC=12$, $BC=5$, and angle $C$ is a right angle. A semicircle is inscribed in the triangle as shown.
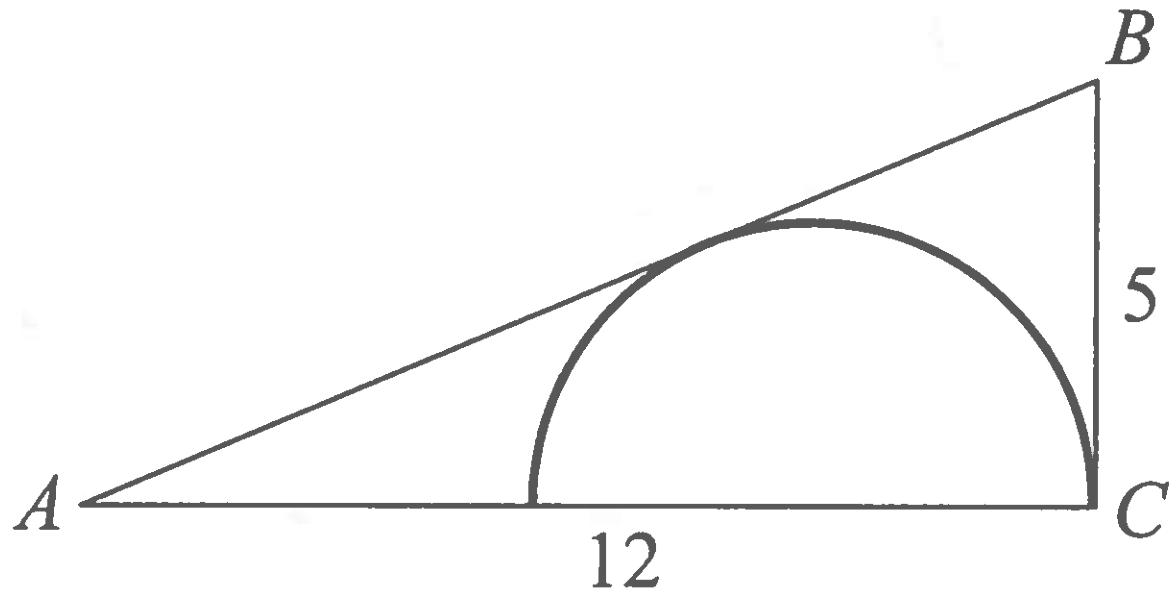
What is the radius of the semicircle?
$\displaystyle \textbf{(A) }\frac{7}{6}\qquad\textbf{(B) }\frac{13}{5}\qquad\textbf{(C) }\frac{59}{18}\qquad\textbf{(D) }\frac{10}{3}\qquad\textbf{(E) }\frac{60}{13}$
Question 23
Each day for four days, Linda traveled for one hour at a speed that resulted in her traveling one mile in an integer number of minutes. Each day after the first, her speed decreased so that the number of minutes to travel one mile increased by $5$ minutes over the preceding day. Each of the four days, her distance traveled was also an integer number of miles. What was the total number of miles for the four trips?
$\textbf{(A) }10\qquad\textbf{(B) }15\qquad\textbf{(C) }25\qquad\textbf{(D) }50\qquad\textbf{(E) }82$
Question 24
Mrs. Sanders has three grandchildren, who call her regularly. One calls her every three days, one calls her every four days, and one calls her every five days. All three called her on December 31, 2016. On how many days during the next year did she not receive a phone call from any of her grandchildren?
$\textbf{(A) }78\qquad\textbf{(B) }80\qquad\textbf{(C) }144\qquad\textbf{(D) }146\qquad\textbf{(E) }152$
Question 25
In the figure shown, $\overline{US}$ and $\overline{UT}$ are line segments each of length $2$, and $m\angle TUS = 60^\circ$.
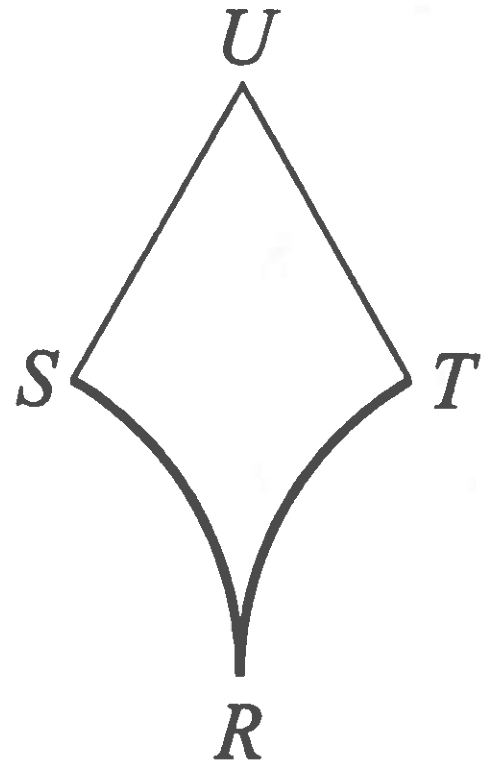
Arcs $\widehat{TR}$ and $\widehat{SR}$ are each one-sixth of a circle with radius $2$. What is the area of the region shown?
$\displaystyle \textbf{(A) }3\sqrt{3}-\pi\qquad\textbf{(B) }4\sqrt{3}-\frac{4\pi}{3}\qquad\textbf{(C) }2\sqrt{3}\qquad\textbf{(D) }4\sqrt{3}-\frac{2\pi}{3}\qquad\textbf{(E) }4+\frac{4\pi}{3}$
Answer can be downloaded using the link: