Phillip just got a new fidget spinner, with ends colored red, blue, and green, as pictured below:
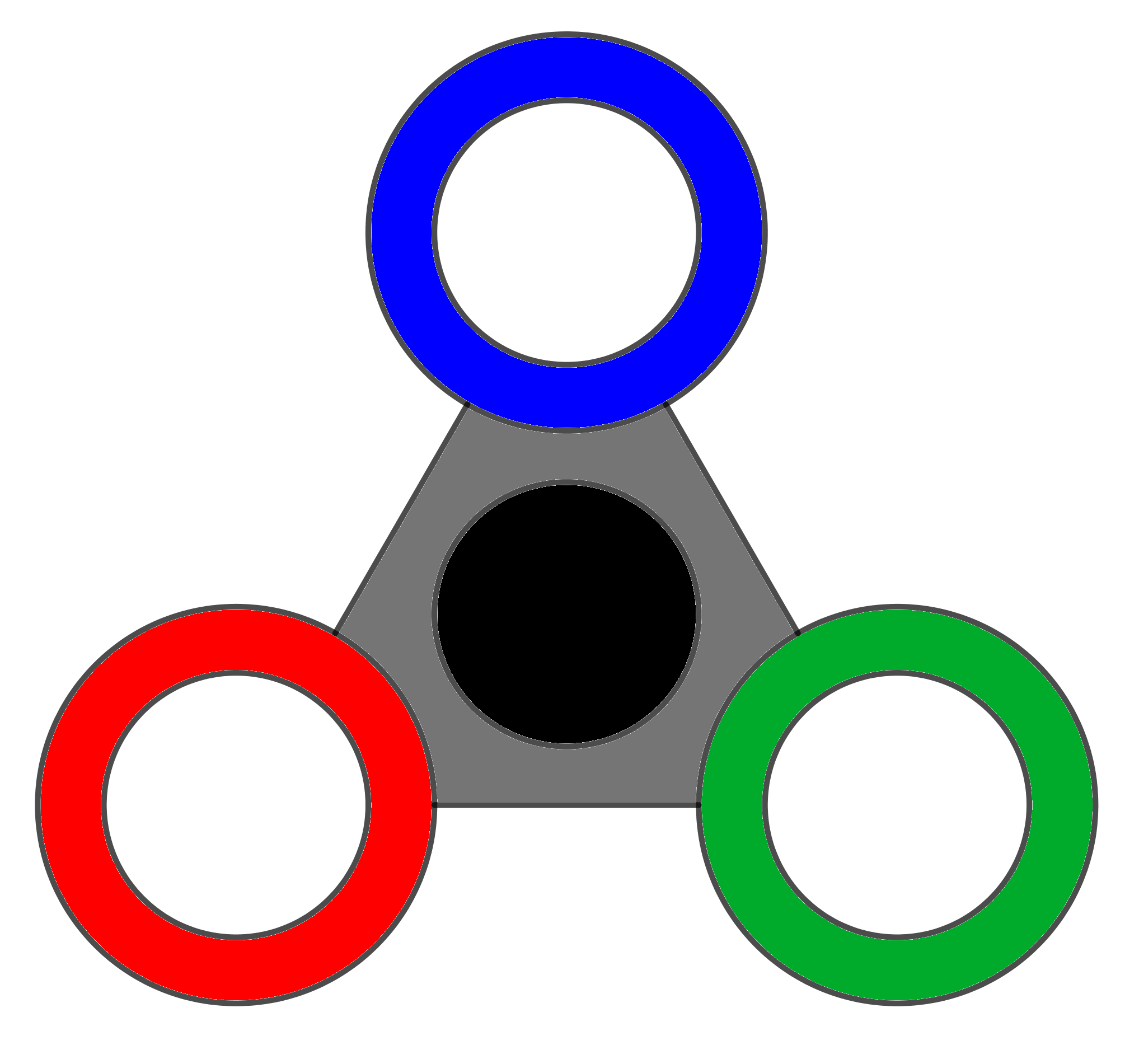
He quickly got bored with just spinning it, but noticed something interesting. He saw that if he spun the spinner $120^\circ$, the fidget spinner, ignoring the colors, would look the same, as we can see below.

He also realized that the same was true if he flipped the spinner horizontally, as shown below:

Phillip explored what arrangements he could get, using only the two operations:
- Rotate $120^\circ$
- Flip horizontally
and came up with the $6$ arrangements below (for example (A) is the original and (B) is the result of rotating by $120^\circ$ once)
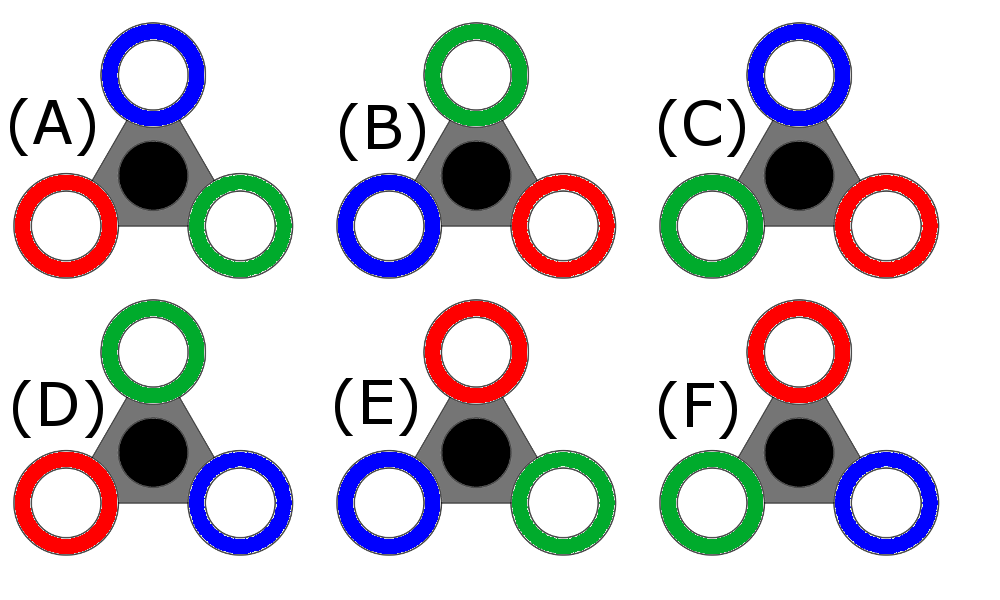
Phillip was a little careless, and forgot exactly how he achieved each of the arrangements. Can you help him by determining the steps/operations (starting with the original and only using the two operations described above) to reach each of the arrangements? Is there only one way to reach each arrangement? What is the minimum number of operations needed?
Please click here to view and participate in this weeks discussion!